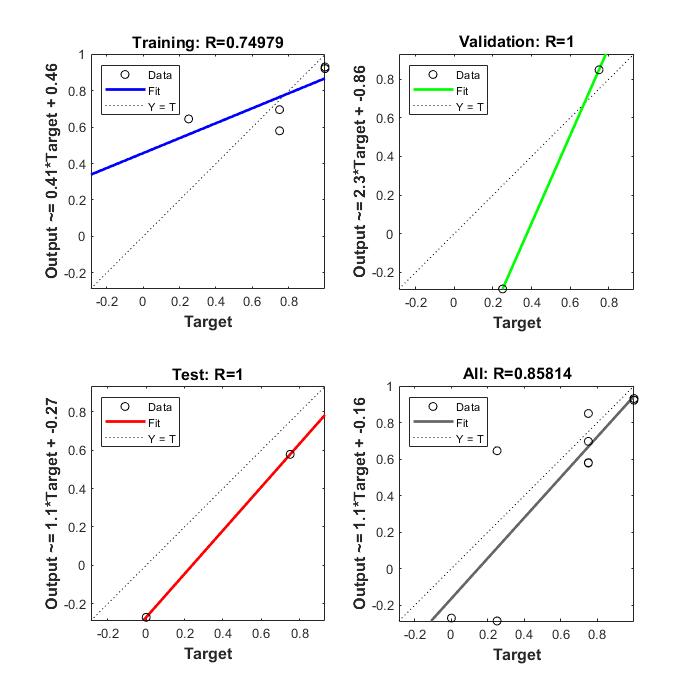
Yapay sinir ağları sinapslara benzer ve bunu temel alarak bir öğrenme modeli oluşturur. Tek katmanlı (single-layer) ve çok katmanlı (multi-layer) olarak iki farklı yapıya ayrılırlar. Çok katmanlı yapay sinir ağlarına birden fazla gizli katman (hidden-layer) ekleyerek daha iyi sonuç elde edebiliriz. Ayrıca hangi aktivasyon fonksiyonunu belirlediğimiz de önemlidir.
Burada verilen bir veri seti üzerinde Matlab’de bu veri setini eğiterek sonuca ulaşmaya çalışacağız.
Bir Elektrik motorunun zamana bağlı ölçülen değerleri aşağıda verilmiştir. Bu
değerleri kullanarak Matlab te ileri beslemeli sinir ağı kullanarak motorun durumunu tespit etmek için m file yazınız. Ağa ait bütün parametreleri komut satırından giriniz. Ayrıca ağırlık ve eşik değerlerini başlangıçta değerlerini rastgele atama yapınız.
Ağın performansını ve Öğrenme durumunu gösteren grafiklerini, giriş verileri ile elde edilenler arasındaki ilişkiyi gösteren
grafikleri ve tercih ettiğiniz ağ topolojisini açıklayınız.
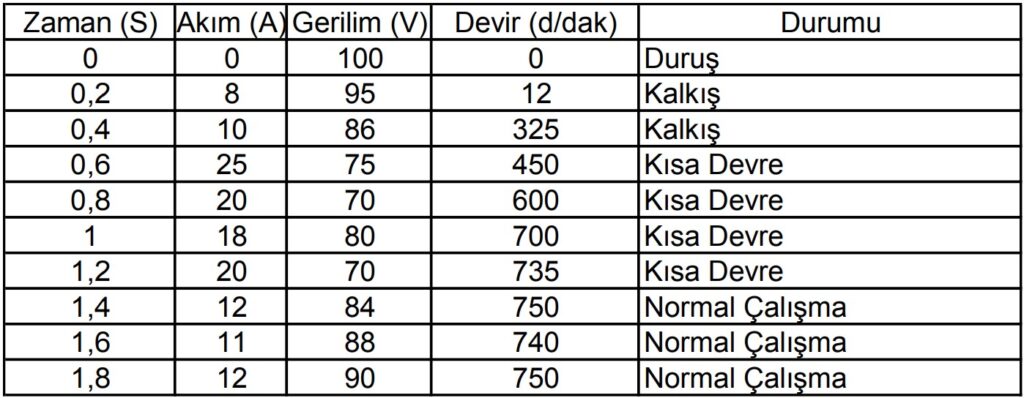
Bize verilen örnek elektrik motorunun zamana bağlı durumu gözükmektedir. Motorun 4 farklı durumu bulunmaktadır. Bunlar duruş, kalkış, kısa devre ve normal çalışma olarak tanımlanmış. Bizlere ileri beslemeli sinir ağı yapısını kullanarak ağı eğitip sonuçlara ulaşmamızı istemiştir. Ayrıca ağa ait sinir hücresi sayısı ve iterasyon değerlerini kendimizin belirlememizi istemiş.
Tabloya baktığımızda zaman içerisinde değişkenlik gösteren 3 ayrı değer ve bunları sonuçları olarak bizlere verdiği 4 adet farklı durumlara sahip 10 birimlik bir vektör bulunuyor. Çözüm olarak matlabı kullanacağız ve verileri elle gireceğiz. Ayrıca veriler bir excel dosyasında oluşturulup matlab’e import edilebilir.
Bizden yalnızca ileri beslemeli istediği istediği için zaman verisini kullanmayacağız. Ancak zaman serisi deseydi timeseriesfeedforwardnet çözümünü kullanabilirdik.
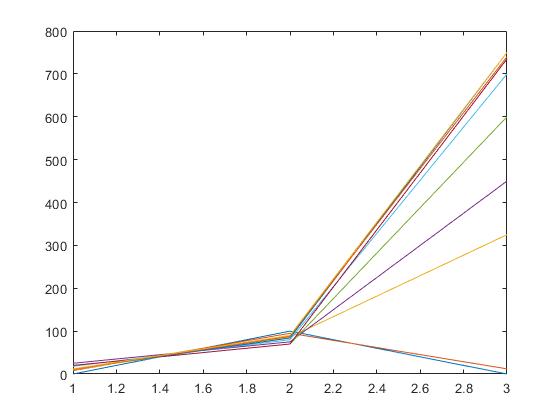
B=[0 8 10 25 20 18 20 12 11 12];
akim=B;
Akım değerlerini sırasıyla girdik
C=[100 95 86 75 70 80 70 84 88 90];
gerilim=C;Daha sonra gerilim değerleri,
D=[0 12 325 450 600 700 735 750 740 750];
devir=D;Son olarak da devir değerlerini sırası ile girdik. Burada dikkat edilmesi gereken vektör uzunluğunun eşit olması gerektiğidir.
Girdiğimiz veriler giriş vektörleridir. Bu vektörlerin tamamını tek bir matrisde gösterelim.
giris=[akim; gerilim; devir;];Giriş verilerini tek bir matrisde gösterdik. Şimdi bizim eğitim için sinir ağına bir hedef (target) verisi vermemiz gerekiyor.
E=[0 0.25 0.25 0.75 0.75 0.75 0.75 1 1 1];
hedef=E;Optimizasyon genelde 0-1 arası yapıldığı için ben de bu şekilde yaptım ancak artan bir vektör olarak göstermemin hata olduğunu da biliyorum. Siz daha iyi optimizasyon yapabilirsiniz.
0 ->Duruş 0,25 ->Kalkış 0,75 ->Kısa devre 1 ->Normal Çalışma
Giriş değerlerini matris içerisinde tanımladık. Çıkış değerlerini de tek boyutlu dizi (vektör) şeklinde oluşturduk. Şimdi sıra sinir hücresi sayısını (ağın boyutunu) belirleyip, giriş verilerinin orta noktasını belirleyip ağırlık değerleri olarak belirlemektir. Bu işlemleri ise;
neuron_size=input('Sinir Hücresi Sayısını giriniz');
net=competlayer(neuron_size);
wts = midpoint(neuron_size,giris)
biases = initcon(neuron_size)Bias değerlerini sinir hücresi sayısı kadar aldık. Şimdi ağımızı oluşturalım.
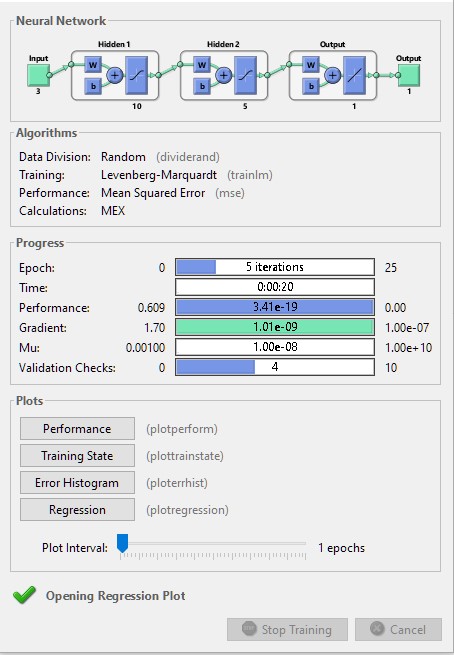
net=feedforwardnet([10 5]);Ağımızı ileri beslemeli sinir ağı olarak eğitmemizi istediği için feedforwardnet() fonksiyonunu kullanıyoruz. Köşeli parantez içerisinde ise gizli katman (hidden-layer) sayısını belirliyoruz. Hidden layerlar daha komplike problemlerde çözüme ulaşmak için de kullanılabilir. Ayrıca hidden-layer olmadan da çözümleme yapabilirsiniz.
Şimdi kullanacağımız iterasyon sayısını kullanıcıdan isteyelim.
epoch_sayisi=input('İterasyon miktarını giriniz:');
net.trainParam.epochs=epoch_sayisi;Kullanacağımız iterasyon sayısını kendimiz belirlememiz problemi ikinci ve üçüncü defa eğitecek olursan hangi iterasyonda çözüme daha fazla yaklaşacağı hususunda bizlere bilgi sağlar. Şimdi eğitimdeki maksimum doğrulama hata sayısını ve eğitimin süresini girelim (inf=infinity).
net.trainParam.max_fail=10;
net.trainParam.time=inf;Şimdi giriş matrisini grafik olarak çizdirelim. Daha sonra sırasıyla ağ, giriş ve hedef verilerini verip ağı eğitelim. Son olarak giriş verilerini ağa vererek eğitilmiş ağın tahmin edilen değerlerini oluşturalım.
plot(giris)
net=train(net,giris,hedef);
y=net(giris)Sinir hücresinin ağırlık ve eşik değerlerini gösterelim. Son olarak ise eğitim de ulaştığımız çıktı değerlerini ve hedef değerlerini art arda gösterip görüntüleyelim.
disp('Çıktılar:');
y
disp('Hedef Değerleri:');
hedefElde ettiğimiz çıktı değerleri aşağıda gösterilmektedir.
Sinir Hücresi Sayısını giriniz5
wts =
12.5000 85.0000 375.0000
12.5000 85.0000 375.0000
12.5000 85.0000 375.0000
biases =
13.5914
13.5914
13.5914
13.5914
13.5914
İterasyon miktarını giriniz:25
y =
Columns 1 through 9
-0.2708 -0.2873 0.6454 0.5802 0.5780 0.8496 0.6967 0.9220 0.9315
Column 10
0.9224
Sinir Hücresinin Ağırlık Değerleri
ans =
-1.3870 1.5663 2.1508
1.4340 -1.9245 -1.8835
1.2740 0.0865 2.6388
-2.1760 1.2914 -1.6081
-1.5975 1.6598 1.9138
-0.0420 2.8726 -1.0065
2.5083 0.2690 -1.6927
-1.0327 -2.3328 -1.6088
0.6780 -2.7898 0.9256
-2.2622 -1.9837 -0.2204
Sinir Hücresinin Eşik Değerleri
ans =
3.0409
-2.2991
-1.7836
1.0313
0.1602
-0.1922
0.9234
-1.6787
2.3483
-3.0124
Çıktılar:
y =
Columns 1 through 9
-0.2708 -0.2873 0.6454 0.5802 0.5780 0.8496 0.6967 0.9220 0.9315
Column 10
0.9224
Hedef Değerleri:
hedef =
Columns 1 through 9
0 0.2500 0.2500 0.7500 0.7500 0.7500 0.7500 1.0000 1.0000
Column 10
1.0000Şimdi ulaştığımız sonuçları gözlemleyelim. İlk değerlerde hedef değerlere göre daha az yakınsayan sonuçlar gözükse de sonlara doğru sonuçlara daha fazla yakınlaştığını görüyoruz.