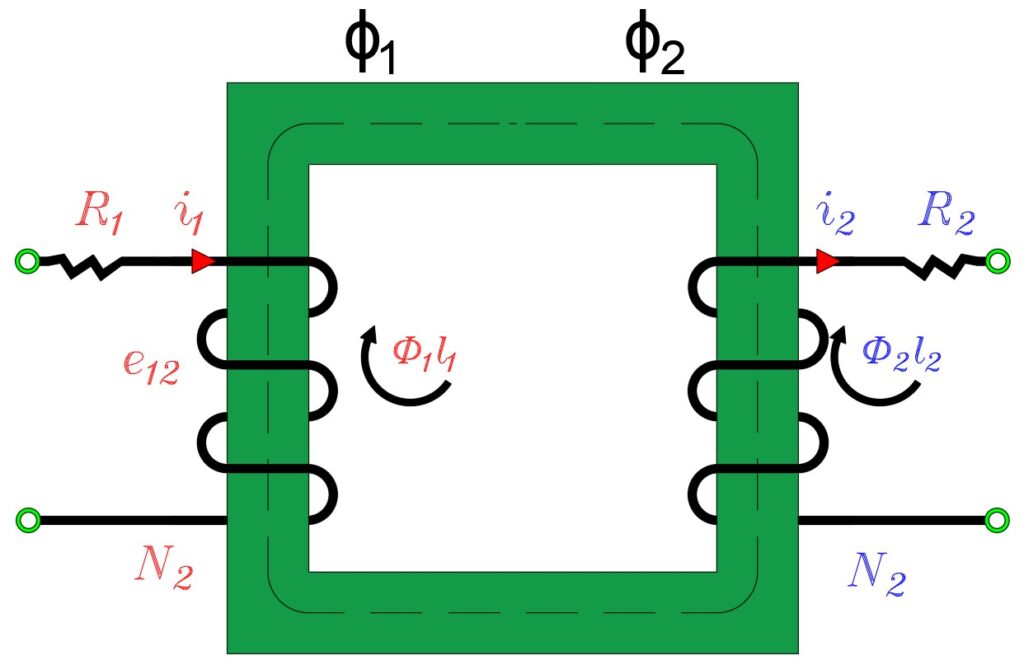
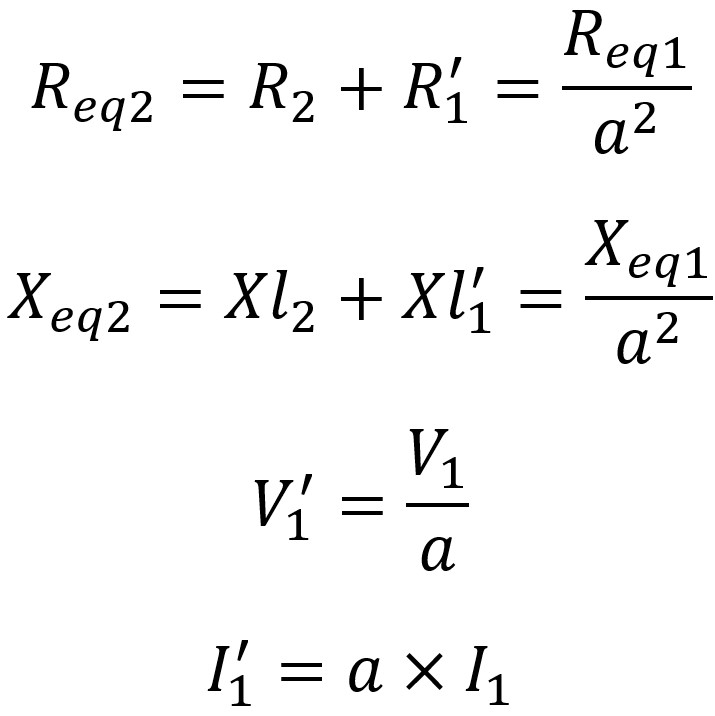POLARİTE
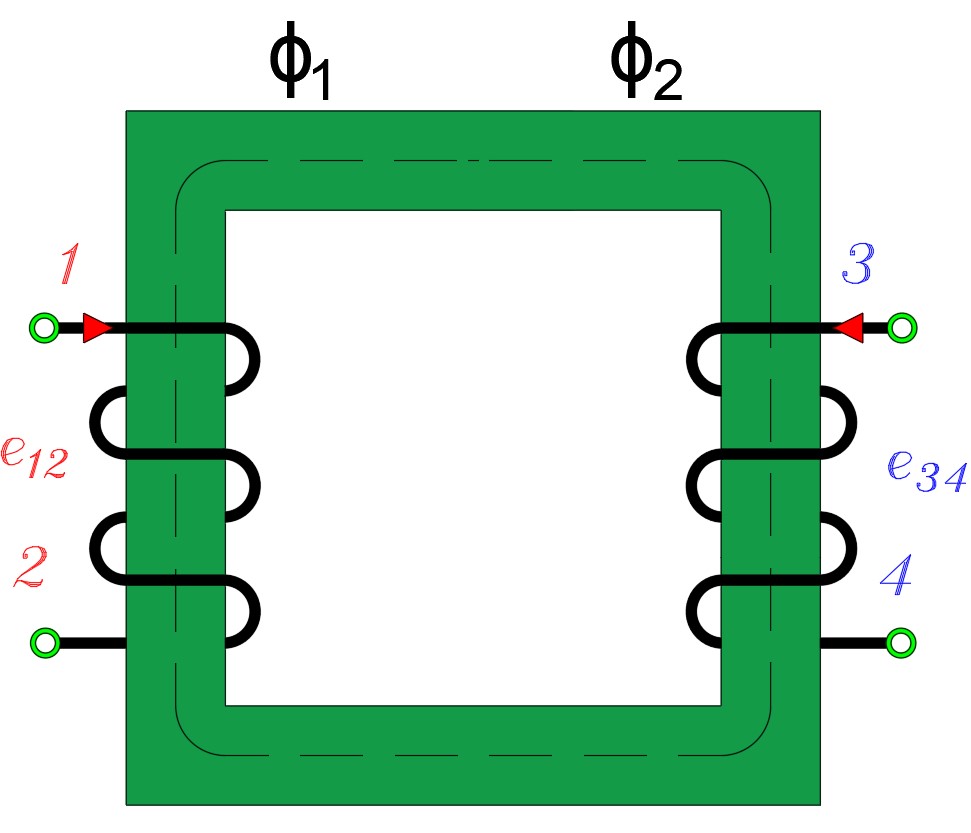
Transformatörlerin sargıları, polariteleri ile ifade edilir. Aşağıdaki şekildeki sargıyı inceleyelim. (1) ve (3) numaralı terminaller birbirine benzer. Her iki terminalden akım içeriye doğru akar. Çekirdek aynı yönde akı oluşturur ve bunlar manyetik yolda akı oluştururlar. Bu durum (2) ve (4) numaralı terminallerde de benzer şekilde oluşur.
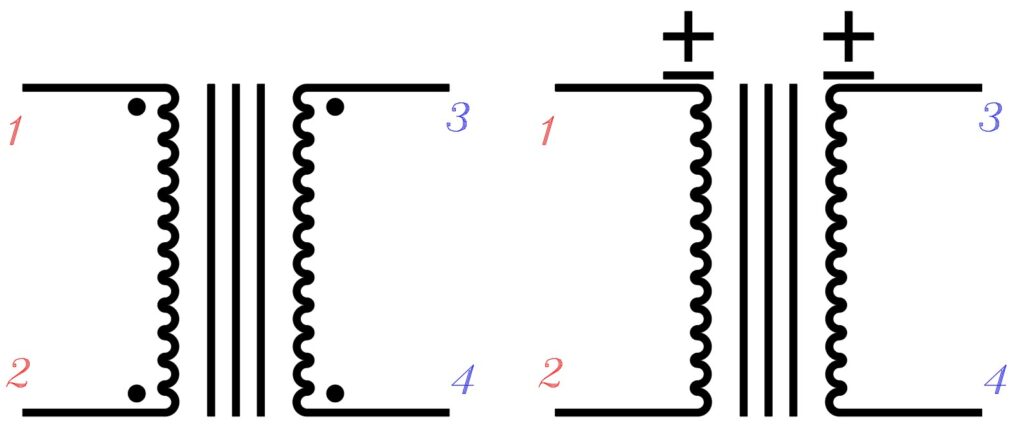
Soldaki: Artı-Eksili gösterim
Endüklenen gerilim e12 ve e34’de aynı fazdadırlar. Bu sebepten 1 ve 2 ile 3 ve 4 yukarıdaki gibi gösterilirler.
PRATİKTE TRANSFORMATÖR
Pratikte bir transformatörde;
- Sargıların dirençleri mevcuttur.
- Her sargı aynı akıyı oluşturmaz.
- Çekirdek malzemesinin permeablitesi homojen değildir.
- Çekirdek kayıpları mevcuttur.
Pratikte, gerçek trafonun analizinde yukarıdaki özelliklerin göz önünde bulundurulması gerekir.
Pratik trafonun analizinde ideal trafodan hareketle iki metot kullanılır:
- Fiziksel yapıdan hareketle bir eşdeğer devre modeli
- Klasik teoriden hareketle manyetik kuplajlı devrelerin matematiksel modeli.
Her iki yöntemde yaygın olarak kullanılır ve döner makine teorisinde birbirine çok yakın sonuç verirler. Fiziksel dönüşümün teorilerini kusursuz karşıladığı için burada eşdeğer devre tekniği kullanılacaktır.
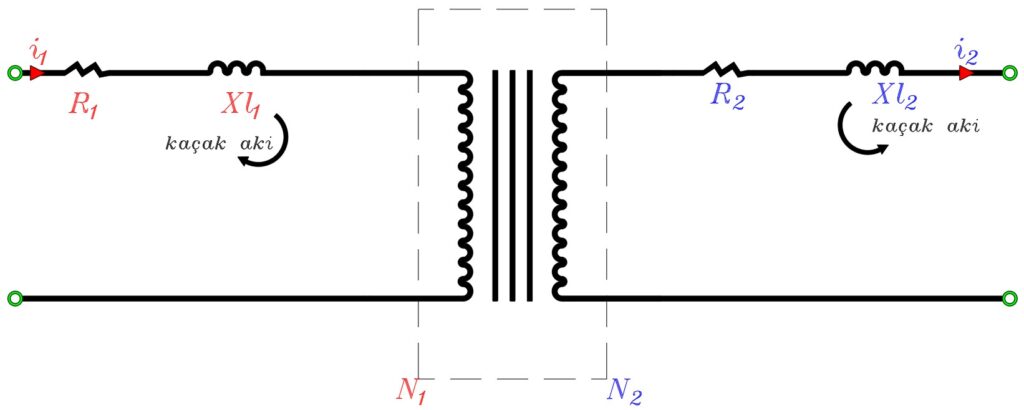
Transformatörlerde ve diğer ferromanyetik malzemelerde, ortak akı Φm’in dışında Φ1 ‘de, yukarıdaki şekilde gösterildiği gibi kaçak akılarda oluşur. Bu akılar, bir sargıda akar ve manyetik devreyi etkilemez. Kaçak yol genellikle havadır ve akan akıma göre değişir (lineer). Kaçak akı genellikle bir endüktans (L) ile sembolize edilir.

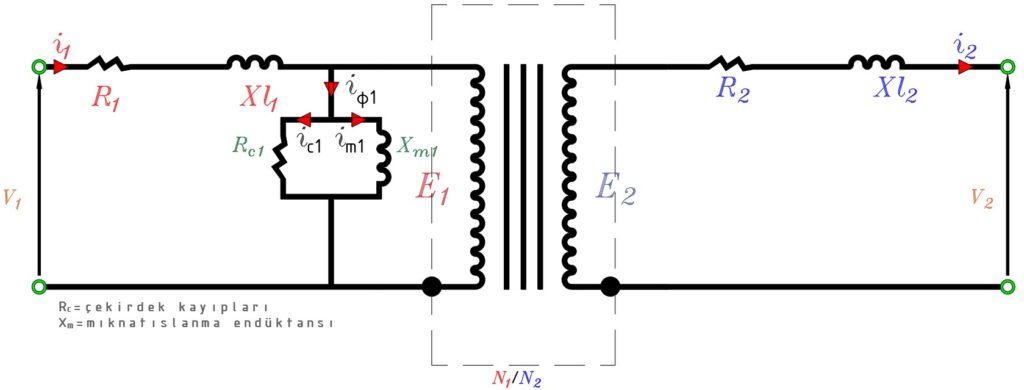
Sargı dirençleri ve kaçak akıların oluşturmuş olduğu endüktanslar ile primer ve sekonder bağlantıları tanımlanmış olur.
Pratik olarak manyetik bir çekirdekte sonlu geçirgenlik ile çekirdekte bir mıknatıslanmayı oluşturmak üzere Im mıknatıslanma akımı akar. Bu olay mıknatıslanma endüktansı Lm ile sembolize edilir. Aynı şekilde çekirdek kayıpları da manyetik malzeme için Rc direnci ile ifade edilir.
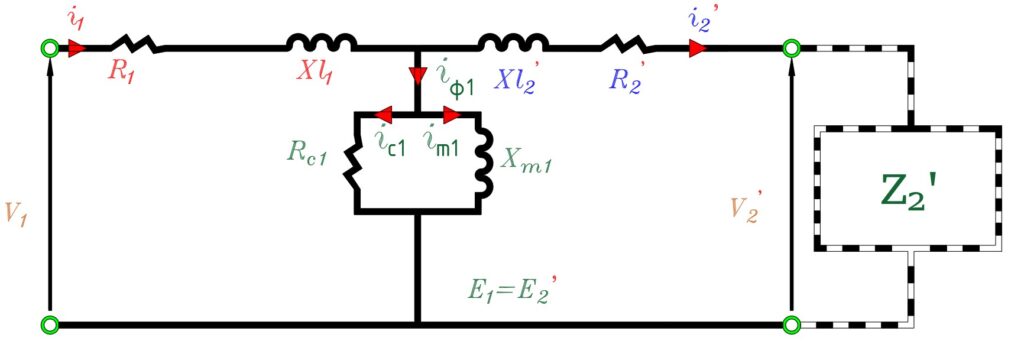
Yukarıdaki şekildeki eşdeğer devre, bu eşdeğer devredeki büyüklükleri sağa ve sola kaydırarak (yani primer veya sekonder tarzla) incelenebilir.
İdeal transformatörün sağa kaydırılmış durumu aşağıdaki resimde incelenebilir.
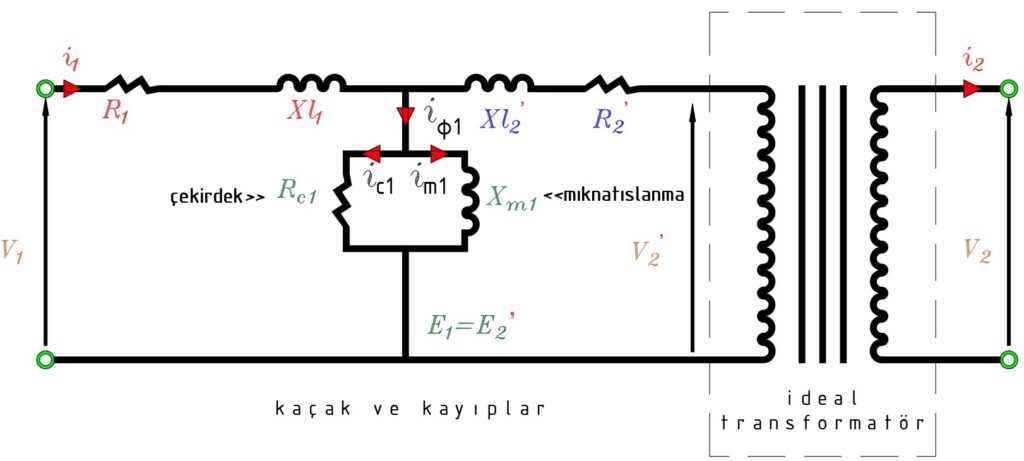
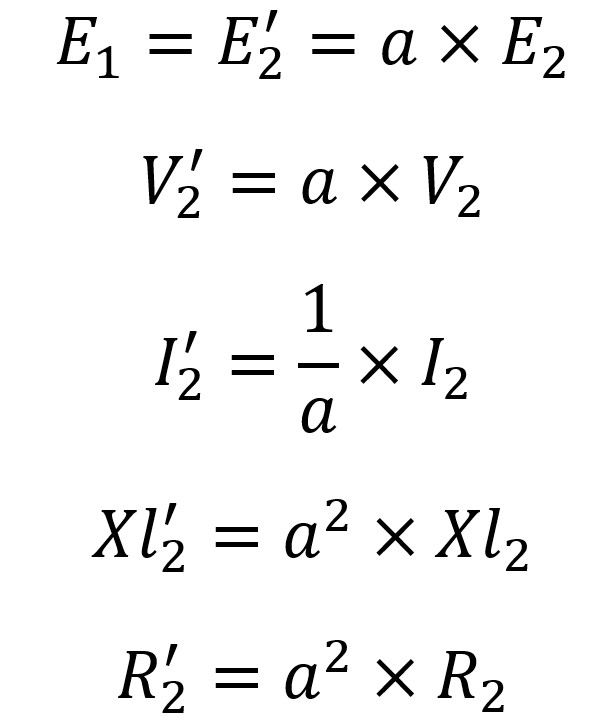
Pratik transformatör, ideal transformatöre ilave olarak, harici endüktanslar çekirdek kayıpları (Rc) ve mıknatıslanma endüktansı (Xm) ile genişletebilir.
EŞDEĞER DEVRELER
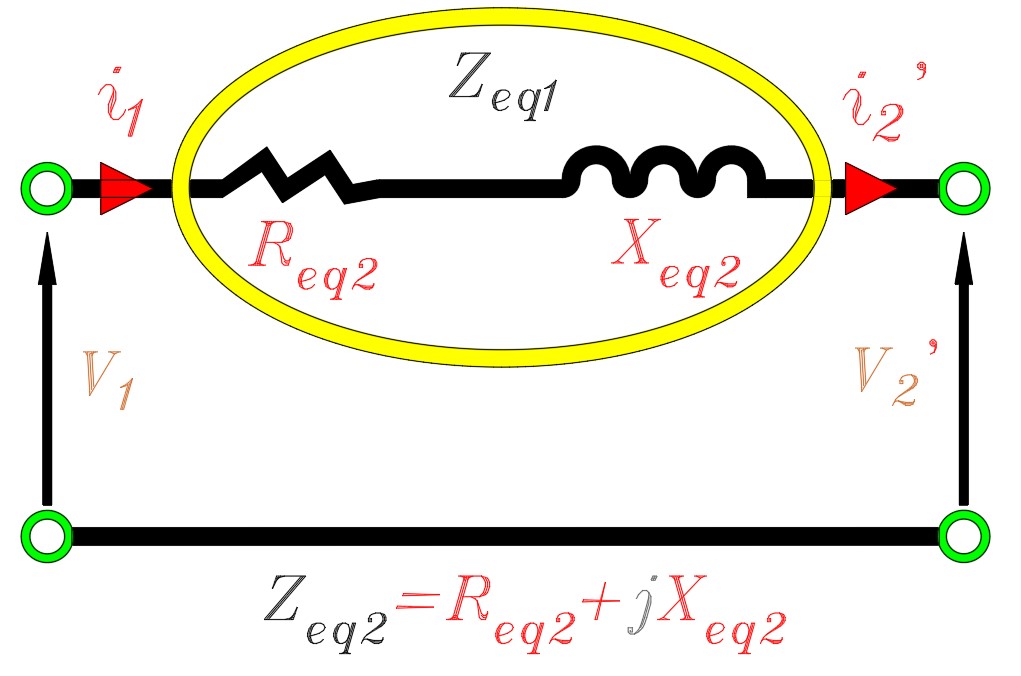
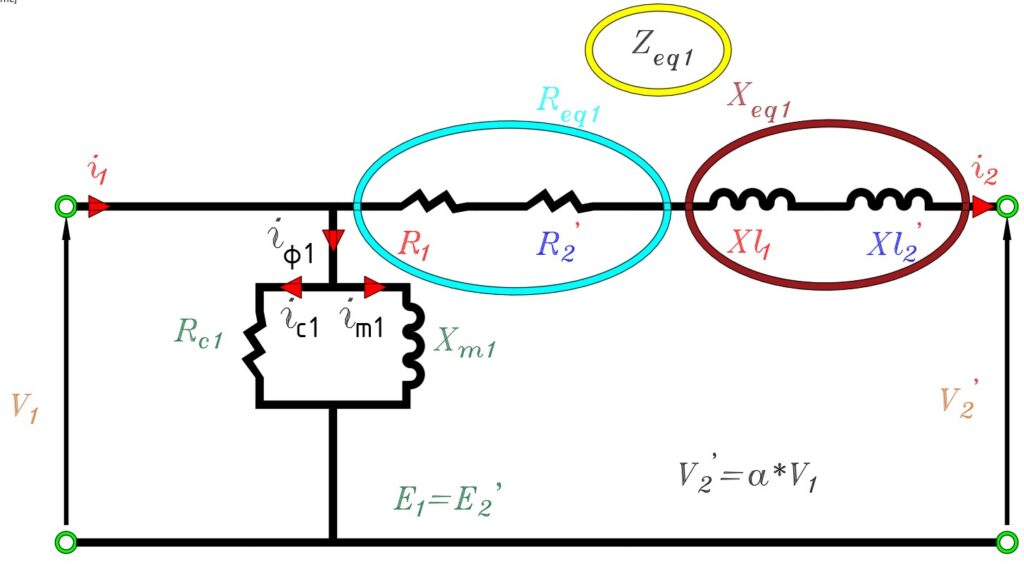
Bütün akım, gerilim ve empedansları bir tarafa geçirerek eşdeğer devre aşağıdaki şekle dönüşür.
Yukarıdaki devredeki tüm değerler giriş kısmına refere edilmiştir. Sarım oranının bilinmesi halinde tüm analizler yapılabilir.
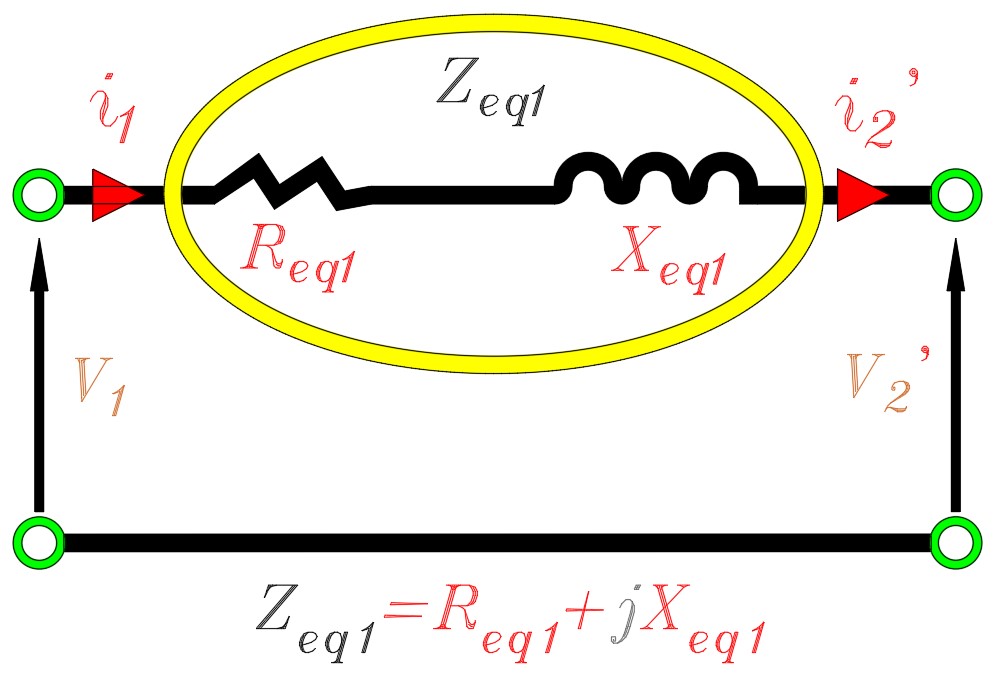
Yaklaşık Eşdeğer Devre
Yukarıdaki resimde görülen i1*R1 ve i1*Xl1 gerilim düşümleri, normalde relatif olarak küçüktür. Ve buradan hareketle,
|E_1 |=|V_1 |
kabulü yapılabilir. Paralel empedans (Rc1 ve Xm1) giriş terminaline taşınabilir. Böylece akımların hesabı kolaylaşır, dirençler ve endüktanslar birleştirilebilir. Bu eşdeğer devre pratik bir transformatörün analizinde kullanılabilir.
PRİMER TARAFIN İNDİRGENMİŞ HALİ
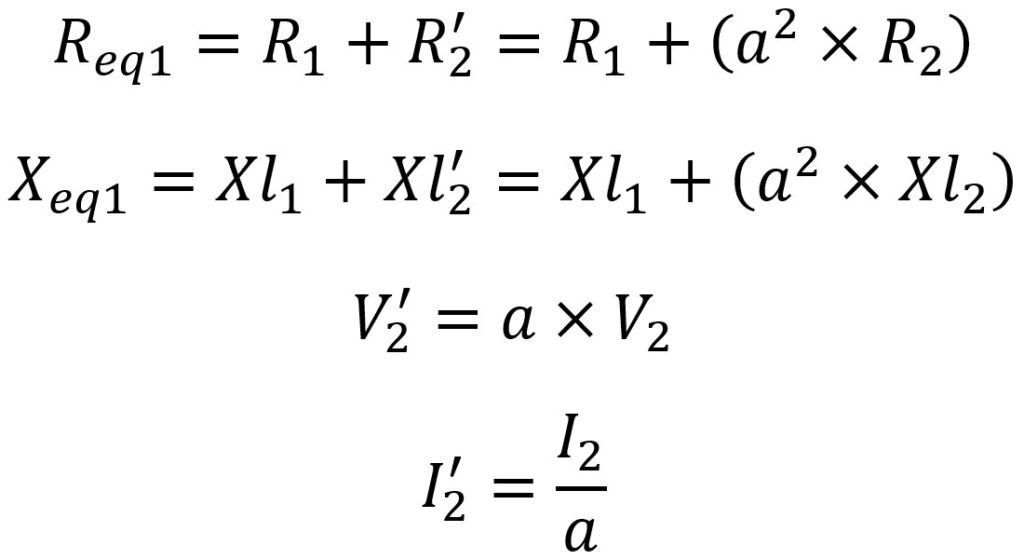
SEKONDER TARAFIN İNDİRGENMİŞ HALİ