2005 yılında Kayseri Erciyes Üniversitesi Öğretim Üyesi Derviş KARABOĞA tarafından nümerik optimizasyon problemlerinin çözümü için geliştirilmiş olup bu problemlerde çok başarılıdır. Yapay arı koloni algoritması optimizasyon algoritmasının arama uzayının farklı alanlarına yayılabilir. Keşif yeteneği, sömürü yeteneğine göre daha başarılıdır.
Bu algoritma doğada arıların bal yapmak için kullandığı yöntemi temele alır. Biz bir kovan içerisindeki arıları kâşif arılar, işçi arılar ve gözcü arılar olarak 3’e ayırıyoruz. Kâşif arılar, kovandan çıkıp rastgele besin kaynağını ararlar. İşçi arılar kâşif arıların bulduğu besin kaynağına gider, eğer bundan daha iyi bir besin kaynağı bulurlarsa ona yönelirler. Gözcü arılar ise kovanda işçi arıların yaptığı titreşimi takip ederek en iyi besin kaynağına yönelirler. Bu arılar besin kaynakları arasından hangisine gideceğine kendisi karar verir.
Kâşif arı rastgele bir şekilde çiçeklerden besin aramaya çıkar. Çiçeklerin üzerindeki besinleri ise kalitesine göre değerlendirir. Eğer besin kaynağı uygunsa kovana geri döner ve yaptığı titreşim hareketleriyle işçi arılara besin kaynağının konumunu tarif ederler. Burada arıların kullanmış oldukları hayretengiz bir yöntem vardır.
Kâşif arılar güneşten gelen açı ile besin kaynağı arasında açı oluşturacak şekilde titreşim dansı yaparlar. Ne kadar fazla titreşim yaparlarsa besin kaynağı o kadar yakın, ne kadar az titreşim yaparlarsa besin kaynağı o kadar uzaktır. Bu titreşim haberleşmesini 1973 yılında Karl von Frisch tespit etmiştir.
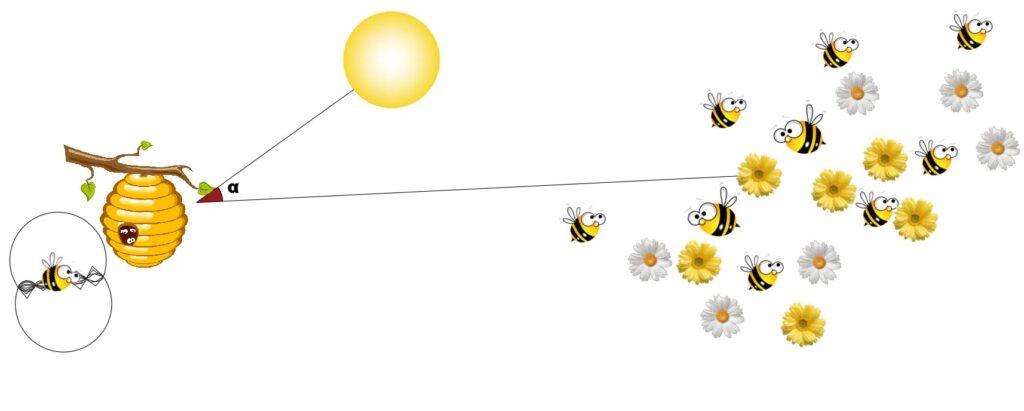
Kovan etrafındaki her bir besin kaynağı muhtemel çözümü ifade eder. Bulunan en iyi besin kaynağı en iyi çözüm demektir. Besin kaynağı tükendiğinde ise işçi ve gözcü arılar kâşif arı gibi hareket ederler.
Yapay Arı Koloni Algoritması
- Kâşif arı safhasında rastgele çözümlerin oluşturulması
- REPEAT
- İşçi arılarca komşu çözümler oluşturulur
- Gözcü arılarca komşu çözümler oluşturulur.
- Başarısızlık sayacında limite ulaşan çözümler silinir ve yerine kâşif arılarca rastgele çözüm türetilir.
- En başarılı çözüm kaydedilir.
- UNTIL
- Sonuç= En başarılı çözüme ulaşılır.
Yapay arı koloni algoritmasını popüler kılan uygulama kolaylığı ve parametre sayısının azlığıdır.
Şimdi bu algoritmayı gezgin satıcı problemi üzerinde deneyelim.
ÖRNEK SORU:
A,B,C,D ve E şehirleri arasındaki mesafeler aşağıdaki mesafe matrisinde verilmiştir. Buna göre yapay arı koloni algoritmasını kullanarak en kısa çözüme ulaşmaya çalışınız. (Besin kaynağı=5 limit=3)
| A | B | C | D | E | |
| A | 20 | 10 | 5 | 8 | |
| B | 20 | 12 | 17 | 13 | |
| C | 10 | 12 | 7 | 10 | |
| D | 5 | 17 | 7 | 10 | |
| E | 8 | 13 | 10 | 10 |
ÇÖZÜM:
İlk olarak buradaki mesafe matrisinden yararlanarak başlangıç verisi olması için rastgele 5 adet çözüm üretiyoruz. Ürettiğimiz her bir çözüm kaynak sayısına denk gelmektedir. Yani elimizde 5 adet kaynak bulunuyor.
- D-B-E-A-C-D=55
- B-C-D-E-A-B=57
- E-D-A-C-B-E=50
- E-B-A-D-C-E=55
- A-E-B-D-C-A=55
Rastgele üretilen çözümler arasında en kaliteli çözüm kaynağı 3. besin kaynağıdır. Yukarıdaki bölüm kaşif arı safhasına girmektedir.
Daha sonra eğer ben bu çözümlerden yeni bir çözüm oluşturmak istiyorsam işçi arı safhasına geçip komşu çözümler oluşturmalıyım.
1. işçi arının 1. ve 3. besin kaynağına gidip 1. ve 3. çözüm kaynaklarını kullanarak yeni bir çözüm ürettiğini varsayalım.
D-B-E-A-C-D=55
E-D-A-C-B-E=50
İki noktalı çaprazlama yöntemi kullanarak 3. ve 5. nodlardan keserek üretilen yeni çözüm ve maliyeti aşağıdaki gibidir.
D-B-A-C-E-D=67
Yöneldiğimiz çözüm 1’di ve bu çözümün maliyeti 55’ti. Arı yeni çözüm üretti ve yeni çözüm daha kötü durumda. 1. çözümün başarısızlık sayacını 1 arttırırız. Başarısızlık sayacı (1)=1 oldu. Bunun yanında mesela 2. işçi arı, maliyeti 57 olan 2. besin kaynağına gitti. Yeni çözüm üretti ve ürettiği çözümün maliyeti 56 oldu. O zaman sonucu 57 olan çözümü iptal edip, 56 olan çözümü tercih eder. 2. çözümün başarısızlık sayacı 0 olur, yani başarısızlık sayacı sıfırlanır.
- başarısızlık sayacı (1)=1 –> daha iyi çözüm bulamadı
- başarısızlık sayacı (2)=0 –> daha iyi çözüm bulundu, eski çözüm silindi.
- başarısızlık sayacı (3)=0 –> daha iyi çözüm bulundu, eski çözüm silindi.
- başarısızlık sayacı (4)=1 –> daha iyi çözüm bulamadı
- başarısızlık sayacı (5)=1 –> daha iyi çözüm bulamadı
Başarısızlık sayacı limite ulaşırsa, işçi arı kaşif arı gibi davranıp rassal çözümler türetir.
Bu aşamadan sonra gözcü arı safhasına geçilir. Gözcü arılar rulet tekerleği yöntemini kullanarak seçim yaparlar. Bu, gözcü arıların daha başarılı çözümü seçme ihtimalini arttırır.
Yapay arı koloni algoritmasında 2 adet parametre vardır. Bunlar, limit ve besin kaynağı parametresi olarak isimlendirilir.
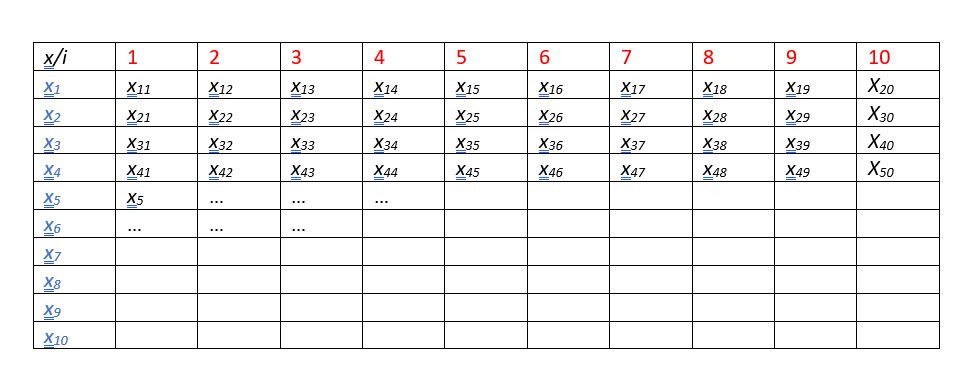
xmi=li+rand(0,1).(ui-li)
x : çözüm matrisi
rakamlar : bu çözüm matrisi içerisindeki …nci eleman.
li : lower bound-alt sınır
ui : upper bound-üst sınır
İşçi arı safhası
vmi=xmi+∅mi(xmi-xki)
∅mi :-1 ile 1 aralığında rastgele bir sayı
xki : rastgele başka bir çözüm seçiyor
gözcü arı safhası
Mevcut çözümleri rulet tekerleğine yerleştiriyor. Hangi çözüme gideceğini kendisi seçiyor.
ÖRNEK SORU
Yapay arı koloni algoritmasıyla ilgili üniversite final sınavımda çıkan bir soruyu ve bu sorunun Excel üzerinden çözümünü yapacağım.

Burada sinüs fonksiyonunun değer aralığını radyan cinsinden yazmalıyız.( π =3,14)
[0-2π]=[0-6,28]
0=>lower bound
6,28=>upper bound
D=5 değerinde olması her bir çözümde 5 adet değer olduğu anlamına geliyor. Ayrıca 5 adet besin kaynağı olması ise 5 adet çözümümüzün olması gerektiğini ifade ediyor. Sonuç olarak elimizde 5*5 boyutunda bir matris olacak.
Yukarıda BAŞLANGIÇ ÇÖZÜMLERİNİN OLUŞTURULMASI bölümünde Başlangıç çözümleri için geçerli, [0,1] aralığındaki rastgele sayılar olarak ifade edilen xmi=li+rand(0,1).(ui-li) formülündeki rand(0,1) bölümüdür. Buradaki rastgele sayılar her öğrenciye göre değişiklik arzedebileceği için hocamız belirli sayılardan oluşan matris oluşturdu.
Bu matrisi kullanarak çözüm matrisini oluşturacağız.
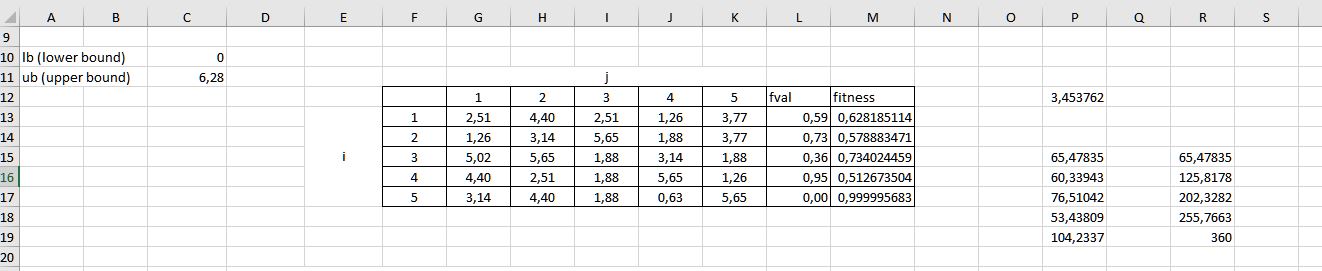
Bize soruda verilen rastgele sayı matrisini (rand(0,1)), lower ve upper bound sayılarını ve oluşturacağımız 5*5’lik çözüm matrisindeki tüm xmi değerlerini de; bu sayılar ve matristeki kutucuklardan alıp tamamlayacak şekilde Excel’e geçirelim.
İlk olarak 0-1 arasındaki rastgele sayı matrisini ve lb ve ub değerlerini [lb=C10, ub=C11]aşağıdaki gibi yerleştirelim.
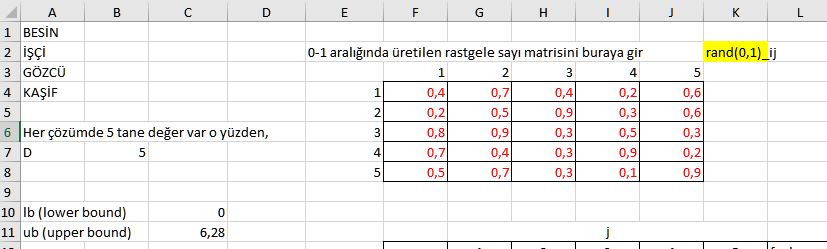
Şimdi xmi=li+rand(0,1).(ui-li) formülüyle başlangıç çözüm matrisini oluşturacağız.
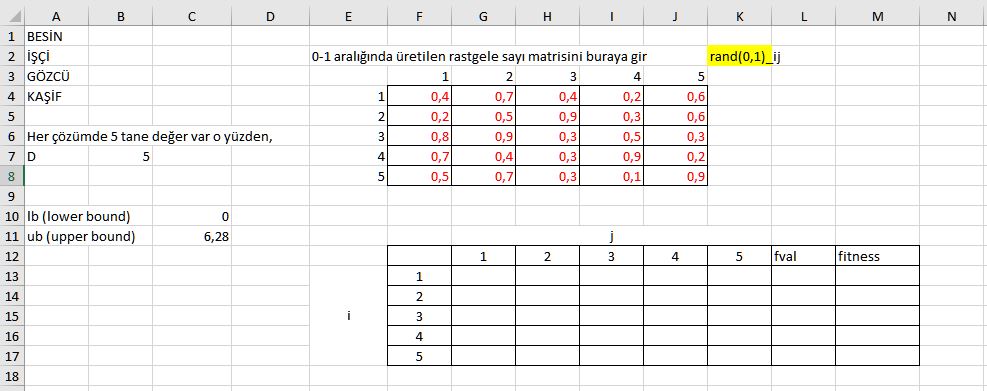
Başlangıç çözüm matrisindeki x11 sayısını bulabilmemiz için l1 sayısını C10 kutucuğundan, ui sayısını C11 kutucuğundan ve rastgele sayı matrisinin rand(0,1)11=(0,4) sayısını F4 kutucuğunun içerisinden seçmemiz gerekli. Formüldeki değer aralığı tüm matris için geçerli olacağı için bu sayıları sabitleyebiliriz. x11 deki kutucuğu seçip yatay ve dikey olarak kaydırma işlemi yapıp formülü tüm matris içerisinde uygulanabilir kılmak için bu işlem gerekli.
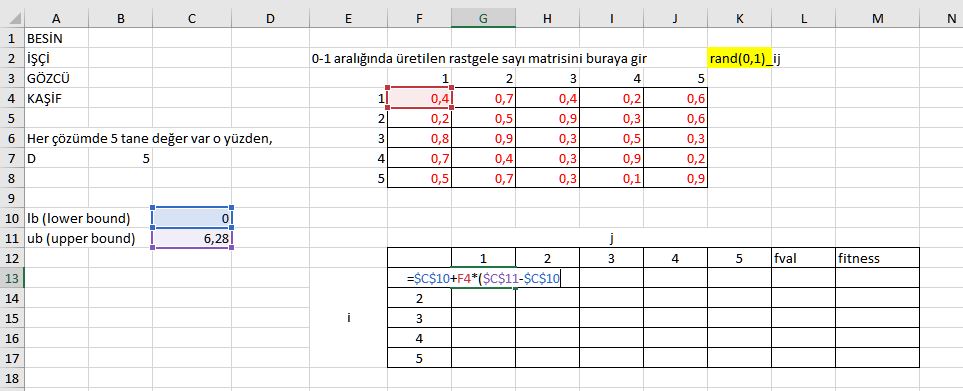
Sonucu G13 kutucuğuna kaydedecektir. Bu kutucuğun sağ alt tarafından tutup aşağıya ve sağa doğru kaydırdığımızda rand(0,1)ij matrisini sabitlemediğimiz için bu matristeki sayılarla eşlenik bir şekilde hesaplama yapacak ve tüm matris içerisindeki sayıların hesaplanmış hali hazır olarak karşımıza çıkacak.
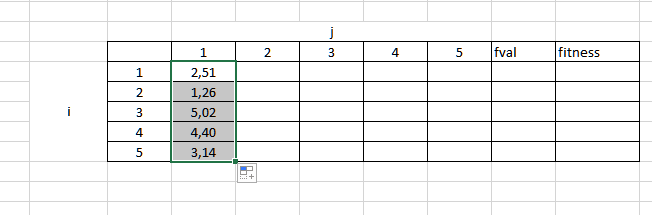
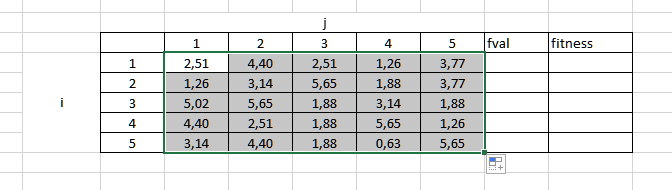
Daha sonra yukarıdaki matriste fval olarak ifade ettiğim fonksiyonu her bir çözüm için hesaplamamız gerekli. Bunun için exceldeki sin() fonksiyonunu kullanmam gerekli. =sin()+sin()… şeklinde 5 tane değeri girip aşağıya doğru kaydırarak sonuca tüm çözümler için ulaşıyorum.
Problem fonksiyonunun altında uygunluk değerini hesaplamamız için verilen değer aralığı mevcut. Hesapladığımız fonksiyon (fval) değeri 0’a eşit veya 0’dan büyükse [1/(1+fval)], 0’dan küçükse [1+|fval|] şeklinde uygunluk değerini bulmamız gerekli.
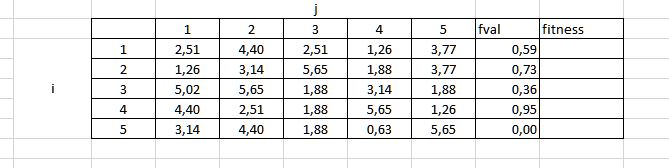
Fonksiyonun hepsinin 0’dan büyük olduğunu görüyorum. Bu yüzden [1/(1+fval)] işlemini gerçekleştirmem gerekli.
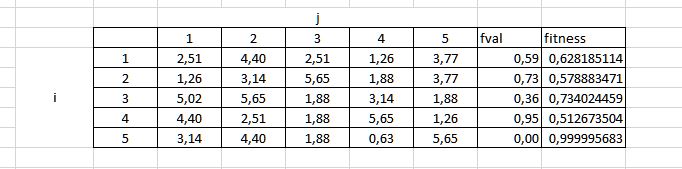
Fonksiyonun BAŞLANGIÇ ÇÖZÜMLERİNİ uygun bir şekilde oluşturduk ve Yapay Arı Koloni Algoritması’nın İşçi Arı Safhâsı’nı gerçekleştirmeye uygun bir şekilde hazırladık.
vmi=xmi+∅mi(xmi-xki)
Problemde İşçi Arı Safhâsı’yla ilgili olarak bizlere rulet tekerleğinin kullanılacağını ifade etmiş ve işçi arı safhasının ilk çevriminde seçilen rastgele açı değerlerini ve rand(-1,1)=>∅mi [-1,1] aralığında üretilen rastgele sayıları bize tablo şeklinde sunmuş.
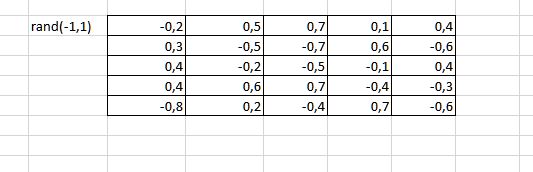
Rastgele sayı tablosunu Excel’e ekledik.
Şimdi bizlere verilen açı değerlerini kullanabilmek için rulet tekerleğine ihtiyacınız var. Rulet tekerleği yöntemini BAŞLANGIÇ ÇÖZÜMLERİ içerisindeki uygunluk (fitness) değerlerini kullanarak elde edeceğiz. 5 adet çözümün uygunluk değerlerini topla() fonksiyonuyla alalım. Daha sonra her bir çözümü toplama bölüp 360 ile çarparak rulet tekerleği içerisinde hangi açı değerine karşılık geldiğini hesaplayalım.
Daha sonra verilen açı değerlerinin olduğu tabloyu Excel’e yerleştirelim. Buradaki rastgele açı tablosunu yerleştirirken rulet tekerleğinde hesapladığımız açılardan kontrolünü sağlayıp kaçıncı çözüme denk geliyorsa o çözümü yazmamız hesaplama kolaylığı açısından bizim için daha uygundur.
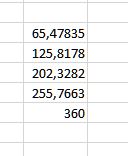
Örneğin; “İşçi Arı 1″in D2‘de rulet tekerleği üzerinde rastgele bir şekilde 105 sayısına denk geldiğini görüyoruz. Bu sayıyı oluşturduğumuz rulet tekerleği üzerinde kontrol ettiğimizde aynı dimension üzerindeki 2. çözüme denk geldiğini görüyoruz. Bu yüzden üreteceğimiz yeni çözümdeki rastgele sayı değerini (xki) 2. çözüm olarak almamız gerekli. Tablodaki açıların da bu şekilde rulet tekerleği üzerinden kontrolünü gerçekleştirip aynı dimension üzerindeki kaçıncı çözüme gideceğimizi bu şekilde bulmalı ve yeni tabloyu Excel üzerinde oluşturmalıyız.
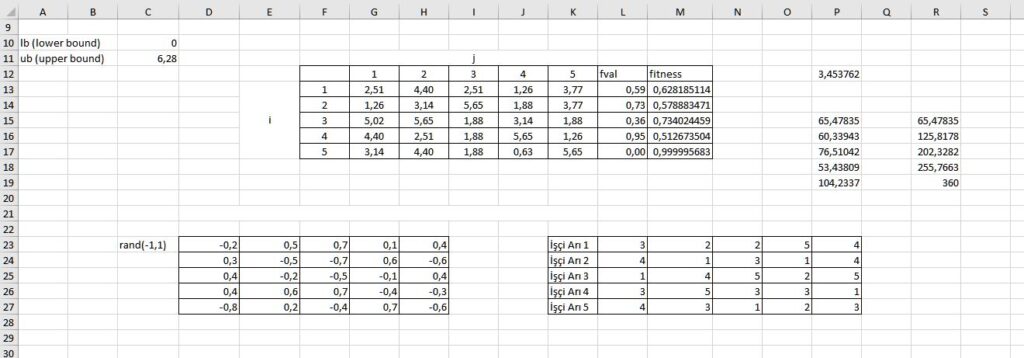
Artık yeni çözüm matrisini oluşturmamız için gerekli veriler elimizde bulunuyor.
Yeni çözüm matrisi için aşağıdaki gibi bir tablo oluşturuyorum.
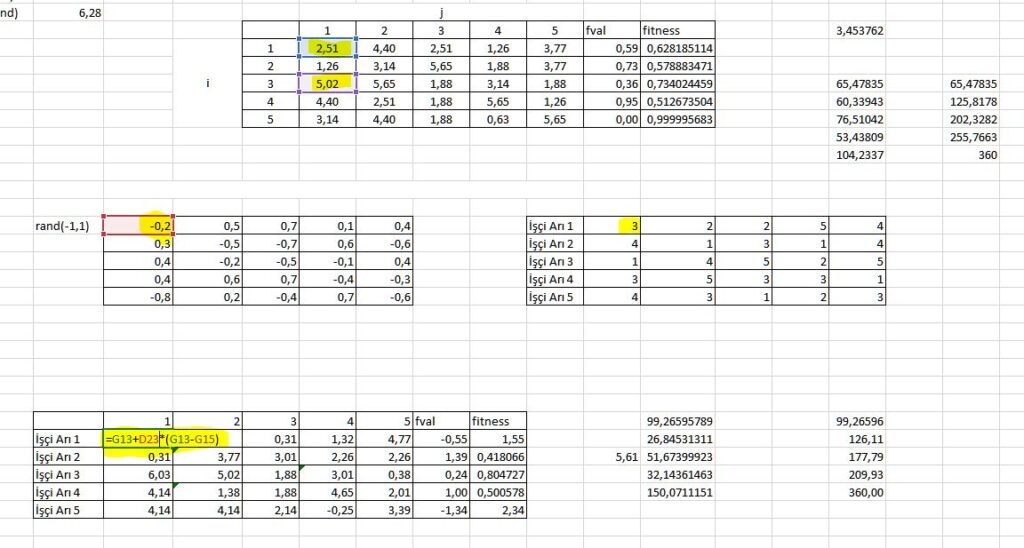
İşçi Arı 1’in 1. dimension’da ürettiği çözüm 2,51. Bu arı aynı dimension içerisinde rastgele 3. kaynağa gittiğini görüyorum. Bu kaynağın sayı değeri 5,02. Burada üretilen -1 ile 1 sayısı rastgele sayı -0,2. Bu durumda uygulayacağımız işlem “=2,51+-0,2(2,51-5,02)”. bu sayıların bulunduğu kutucukları işaretleyerek sonuca ulaşabiliriz. Farklı bir fonksiyon kullanılarak da bu işlem yapılabilir ancak hangi kaynağa gittiğine matristen bakıp bunları tabloya işlemek daha kısa sürüyor.
Tabloda oluşan çözümlerin fval değerini hesaplamalı daha sonra bu fval değerlerini kontrol ederek uygunluk fonksiyonunu oluşturmamız gerekli. Burada İşçi Arı 1’in fval değerinin -0,55 olduğu için uygunluk fonksiyonu 1+abs(-0,55) şeklinde olmalı.
Excelde 1+MUTLAK(-0,55) veya 1+MUTLAK(I35) şeklinde yazmalıyız.
Tüm çözümler için uygunluk fonksiyonu oluştuğuna göre rulet tekerleğini yukarıda görüldüğü gibi oluşturabiliriz.
2 adet çözüm matrisi oluşmuş oldu. Bunlardan birisi BAŞLANGIÇ ÇÖZÜM MATRİSİ ikincisi İŞÇİ ARI SAFHASININ İLK ÇÖZÜMÜ MATRİSİ. Bizim bu safhanın ikinci çevriminde iki matriste üretilen çözümlerin fval değerlerini karşılaştırıp en düşük maliyetli olan hangisiyse o çözümü alıp yeni bir çözüm matrisi oluşturmamız gerekli.
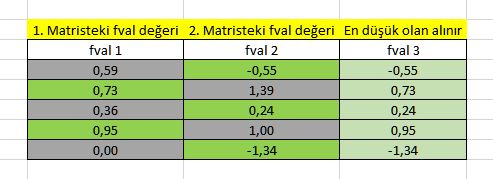
Buna göre İŞÇİ ARI SAFHASININ 2. ÇEVRİMİNİN çözüm matrisi, fval değeri, uygunluk fonksiyonu ve rulet tekerleği de aşağıda görüldüğü gibi oluşur.

Yukarıdaki soruda bizden istenilen tüm aşamaları gerçekleştirip çözümlere ulaşmış olduk.
Bu yazımızda Yapay Arı Koloni Algoritması’nın ortaya çıkışı, algoritmanın yapısı ve algoritmayla ilgili kapsamlı bir örnek uygulama yapılması adımlarını sırasıyla gerçekleştirdik.
