Karınca Koloni Optimizasyonu karıncaların yiyecek araştırması sırasında kullandıkları yöntemler gözlenerek oluşturulmuştur. Karıncalar besin bulmak için yuvalarından çıkarlar. Besine ulaşan karıncalar besinin kalitesi, besin ile yuva arasındaki mesafe gibi bir çok bilgiyi diğer karıncalara ulaştırırlar. Bu bilgilerin ulaştırılması biyolojik olarak feromon adı verilen hormon aracılığıyla gerçekleşir. Feromon, aynı tür üyeler arasındaki sosyal ilişkileri düzenleyen, dışarıya kokuyla yayılan hormon çeşidine verilen isimdir. Besine ulaşan karınca eğer besin kaliteliyse burada feromon salgısı oluşturur. Ardından gelen karıncaların da bu salgıyı oluşturmasıyla birlikte yuva ile besin arasındaki yolda feromon yoğunluğu oluşmaya başlar ve diğer karıncalar da bu yoğunluğa yönelirler. Feromon hormonu, yuva ile besin arasındaki en kısa mesafenin oluşturulmasında da kullanılır.(bkz.2)
1989 yılında düzenlenen iki deneyden birinde karıncaların yuva ile besin arasındaki iki eşit mesafeden birini tercih etmesi gözlendi. Karıncalar rastgele bir şekilde iki ayrı yolda da yoğunlaşmıştı. Diğer deneyde ise biri diğerinden iki kat uzun iki ayrı yoldan birini tercih etmesi gözlenen karıncaların kısa yolda yoğunlaştığı gözlemlendi.(bkz. 1)
Karınca koloni optimizasyonu 3 ayrı algoritmadan oluşur.
- Ant Sistem (Karınca Sistemi) Algoritması
- Karınca Koloni Algoritması- ACS (Ant Colony Alghorithm)
- Min-Max Ant Sistem Algorithm
Karınca Sistemi (Ant System) Algoritmasının Gezgin Satıcı (Traveling Salesman) Problemi üzerinde uygulanması için geliştirilmiş formüller bulunmaktadır.
Bir k karıncasının t iterasyonunda i noktasından j noktasına gitme olasılığı pijk(t) olarak gösterilir.
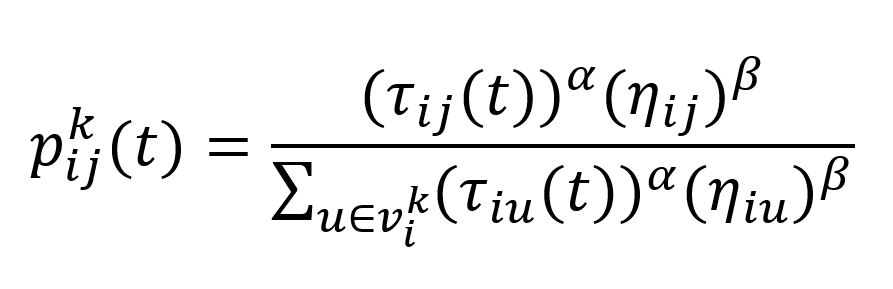
τiu= yeni feromon
- ηij=minimizasyon problemi olduğu için 1/(mesafe)
- τiu= yeni feromon
- Alfa (α) Parametresi=Düğümler arası feromonun göreceli önemini belirleyen parametre
- Beta (β) Parametresi=Düğümler arası mesafenin önemini belirleyen parametre
- Tau (?) Parametresi=Düğümler arasındaki feromon miktarını belirleyen feromon matrisidir. Feromon miktarı ilk başta çok düşük seviyelerde belirlenir.
- Ro (ρ) Parametresi=Feromonun buharlaşma-uçuculuk katsayısıdır.(bkz. 3)
Karınca sistemi (KS)- Ant System (AS) Algoritması
- Parametre değerlerinin belirlenmesi (α, β, ?, ρ)
- Başlangıç feromon değerlerinin atanması
- Başlangıç çözümlerinin oluşturulması
- REPEAT
- Feromon miktarlarının güncellenmesi
- Yeni çözümlerin inşa edilmesi
- En iyi çözümün hafızaya alınması
- UNTIL(bkz. 4)
Yine gezgin satıcı problem içerisinde bir örnek yapalım
A, B, C, D ve E şehirleri arasında herhangi bir şehirden aldığı malı yine aynı şehre geri dönerek tamamlayan mesafe matrisi verilmiştir. Parametre değerlerini belirleyip, başlangıç feromon matrisini oluşturun. Rastgele mesafelerden oluşan başlangıç çözümlerini oluşturun.
| A | B | C | D | E | |
| A | 20 | 10 | 5 | 8 | |
| B | 20 | 12 | 17 | 13 | |
| C | 10 | 12 | 7 | 10 | |
| D | 5 | 17 | 7 | 10 | |
| E | 8 | 13 | 10 | 10 |
Daha sonra oluşturacağımız parametre değerlerinden alfa (α) değeri genellikle 1,3 veya 5 değerlerinden herhangi bir tanesi seçiliyor.
Beta (β) değeri ise genellikle 5 olarak seçiliyor.
Ro (ρ) değeri dediğimiz feromonun uçuculuk katsayısı ise genellikle 0,1 olarak alınıyor.
Oluşturacağımız feromon matrisi 0’dan büyük ancak çok küçük değerlerde olmalı bunun için ilk olarak feromonları her bir nod için 0,1 olarak belirliyorum.(bkz. 5)
| A | B | C | D | E | |
| A | 0,1 | 0,1 | 0,1 | 0,1 | |
| B | 0,1 | 0,1 | 0,1 | 0,1 | |
| C | 0,1 | 0,1 | 0,1 | 0,1 | |
| D | 0,1 | 0,1 | 0,1 | 0,1 | |
| E | 0,1 | 0,1 | 0,1 | 0,1 |
Yukarıda bize verilen mesafe matrisini görmekteyiz. Bu matrise göre rastgele bir şekilde başlangıç çözümlerini oluşturuyorum.
A-C-E-B-D-A=55
B-E-A-D-C-B=45
C-B-A-D-E-C=57
D-A-E-C-B-D=52
E-D-B-C-A-E=57
Algoritma sırasına göre ilk olarak parametre değerlerini belirledim, daha sonra feromon matrisini oluşturdum. Son olarak ise rastgele bir şekilde başlangıç değerlerini belirledim.
Şimdi ise daha iyi çözümler oluşturup en iyi çözüme ulaşmak için algoritmanın diğer aşamalarını gerçekleştirelim.
Yeni feromon değerlerini bulurken;
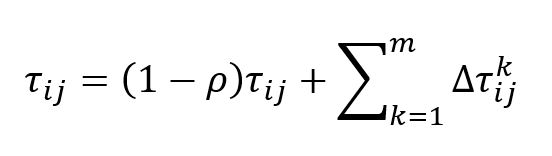
?ij= i nodundan j noduna gidişin feromon matrisindeki karşılığının değeri
Δ?ij= i’den j’ye giden nodlar (örneğin C-D), oluşturulan başlangıç değerleri (çözümleri) içerisinden kontrol edilir. Başlangıç çözümü içerisinde eğer bu noddan mevcutsa o çözümün 1/maliyetini dahil ediyoruz. Eğer bulunmuyorsa 0 ekliyoruz. Oluşturduğumuz başlangıç çözümlerindeki tüm nodları tek tek kontrol etmeliyiz.(bkz. 6)
Şimdi yukarıdak başlangıç çözümleri içerisinden sırasıyla tüm nodları kontrol edip bulduğumuz feromon değerlerinden yeni feromon matrisini oluşturalım.
?AB= (1-0,1)0,1=0,09 (AB nodu başlangıç çözümleri içerisindeki hiçbir çözümde bulunmuyor)
?AD= (1-0,1)0,1+[(1/45)+(1/57)]=0,13 (AD nodu 2. ve 3. başlangıç çözümleri içerisinde bulunuyor)
?AC= (1-0,1)0,1+(1/55)=0,108 (AC nodu yalnızca 1. başlangıç çözümü içerisinde bulunuyor)
Bu şekilde tüm nodları hesapladığımızda oluşan yeni feromon matrisi;
| A | B | C | D | E | |
| A | 0,09 | 0,108 | 0,138 | 0,126 | |
| B | 0,107 | 0,107 | 0,127 | 0,112 | |
| C | 0,107 | 0,126 | 0,09 | 0,108 | |
| D | 0,127 | 0,112 | 0,112 | 0,107 | |
| E | 0,112 | 0,108 | 0,127 | 0,107 |
Yukarıdaki yeni feromon matrisine baktığımızda A ile B arası nodun karıncalar tarafından kullanılmaması sebebiyle buradaki feromon değerinin düştüğünü gözlemleyebiliriz. A ile D arasındaki feromon değerine baktığımızda ise buranın 2. ve 3. karıncalar tarafından kullanıldığını görüyoruz. Bundan dolayı A-D nodunun feromon değeri artış göstermiştir. Bir sonraki iterasyonda A-B düğümünün seçilme olasığı azalırken A-D nodunun seçilme olasılığı azalıcak.
Şimdi yukarıda öğrendiğimiz karıncanın bir düğümden başka bir düğüme gitme olasılığını hesaplayalım;
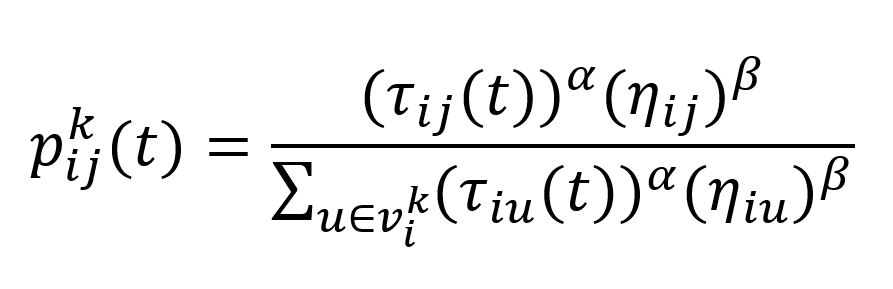
Formüle göre A’da bulunan bir karıncanın B düğümüne gitme ihtimali;
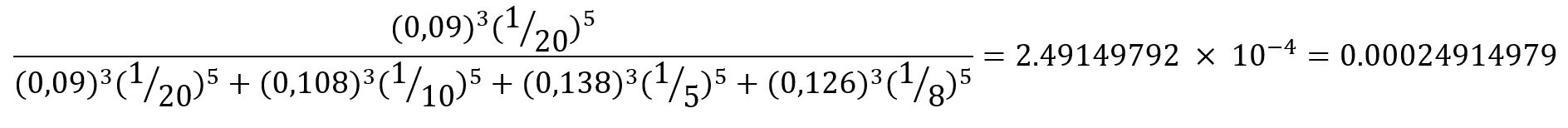
KAYNAKÇA
- aco-book.pdf (cmu.edu)
- Ant System (ab.org.tr)
- (PDF) Ant Algorithms: Theory and Applications (researchgate.net)
- Multiobjective Optimization in Optical Networks – ScienceDirect
- Optimization of Methods for Image-Texture Segmentation Using Ant Colony Optimization – ScienceDirect
- Metaheuristics for the tabu clustered traveling salesman problem – ScienceDirect
