Optimizasyon tekniği, fonksiyonun minimum ve maksimum noktasını belirlemede kullanılır. Eğer problem minimizasyon problemiyse minimum değerler (maliyet) noktası bulunacak. Maksimizasyon problemlerinde ise maksimum değerler (maliyet) noktası bulunacak. Buradaki maksimum veya minimum noktaları sezgisel veya meta-sezgisel algoritmalar yoluyla buluyoruz.
Optimizasyon Teknikleri’nde, Yapay Zeka optimizasyonundan bahsedeceğiz ve karşımızdaki milyonlarca veya milyarlarca çözüm içerisinden optimum çözümü bulmaya çalışan algoritmalar kullanacağız ya da optimumu arayan teknikler üzerinde çalışacağız.
Optimizasyon problemlerini nümerik (continous) optimizasyon problemleri ve ayrık (discrete) optimizasyon problemleri olarak ikiye ayırabiliriz. Nümerik (continous) optimizasyon problemlerine minimum maksimum noktayı bulma problemleri, Ayrık (discrete) optimizasyon problemlerine ise araç rotalama problemleri ve gezgin satıcı problemlerini örnek olarak verebiliriz.
50 kg yük taşıyan bir araç çeşitli illerden geçerek kargosu olan illeri Düzce’deki toplama noktasına getirmektedir.
ÖRNEK SORU 1
- Bilecik
- Bolu
- Düzce
- Karabük
- Kocaeli
- İstanbul
- Sakarya
| Toplanma | Dağıtım | Ağırlık |
| Karabük | Sakarya | 20 |
| Karabük | Kocaeli | 15 |
| Bolu | İstanbul | 25 |
| Sakarya | İstanbul | 20 |
Düzce’den yola çıkıp Bolu’dan 25 kilogram yük alan araç daha sonra Karabük’e uğrayamaz çünkü aracın maksimum taşıma kapasitesi 50 kilogramdır. Bu araç Bolu’dan sonra sadece Sakarya’ya uğrayabilir.
ÖRNEK SORU 2
Maksimum hacmi 50m3 ve maksimum taşıma ağırlığı 100 kg olan bir sırt çantasına aşağıdaki hacim ve ağırlığa sahip 6 adet cisim yerleştirilecektir. Çantanın içerisine cisimler 1, konulmayan cisimler 0 ile numaralandırılacaktır. Oluşan dizinin, çantanın boyutunu aşıp aşmadığı ile ilgili değerlendirme yapılacaktır.
- A) 10m3/15kg
- B) 15m3/5kg
- C) 20m3/25kg
- D) 25m3/15kg
- E) 15m3/10kg
- F) 20m3/10kg
1–> Çantada var
0–> Çantada yok
1-1-0-1-0-0 h=50m3, a=35kg, k=70
1-0-1-1-1-1 Hacim aşıyor. Çözüm değil.
Optimizasyon teknikleri, içerisinde 100’lerce algoritma bulunan ve gün geçtikçe yeni algoritmaların yayınlandığı çok geniş bir konudur. Biz Optimizasyon Teknikleri çatısı altında 3 farklı optimizasyon algoritması ele alınacaktır. Bunlar;
- Genetik Algoritmalar (Genetic Algorithms)
- Karınca Koloni Algoritması (Ant Colony Algorithms)
- Yapay Arı Koloni Algoritması (Artificial Bee Colony Algorithms)
Genetik Algoritmalar (Genetic Algorithms)
Genetik Algoritmaların temeli John Henry Holland tarafından atılmıştır. Genetik algoritmada ilk olarak başlangıç popülasyonları oluşturur. Daha sonra döngü içerisinde fonksiyonun durumuna göre çaprazlama, mutasyon, doğal seleksiyon işlemleri tekrar edilir.
Genetik Algoritma Aşamaları:
- Başlangıç Popülasyonunu Oluştur
- REPEAT
- Çaprazlama
- Mutasyon
- Doğal Seleksiyon
- UNTİL
Bu konuyu yine Gezgin Satıcı Problemi üzerinden vereceğimiz örneklerle inceleyeceğiz.
ÖRNEK SORU 2
A, B, C, D ve E şehirlerinin arasındaki mesafeler aşağıdaki mesafe matrisinde verilmiştir. Genetik Algoritma tekniğini kullanarak en düşük maliyetli çevrimi bulunuz. (Başlangıç popülasyonu 5, çaprazlama oranı %80, mutasyon oranı %20 )
| A | B | C | D | E | |
| A | 25 | 10 | 30 | 30 | |
| B | 25 | 20 | 35 | 10 | |
| C | 10 | 20 | 25 | 30 | |
| D | 30 | 35 | 25 | 30 | |
| E | 30 | 10 | 30 | 30 |
5 adet başlangıç popülasyonu oluşturmamız gerektiği soruda bizlere ifade edildiğinden ilk olarak bunu oluşturmamız gerekli. Popülasyon kromozomlardan, kromozomlarsa genlerden meydana gelir.
Burada rastgele oluşturacağımız bir C-E-A-D-B-C rotasına kromozom, bu kromozomun çözüm elemanlarından herhangi bir tanesine, meselâ B elemanına gen adı veriliyor.
Peki oluşturduğumuz C-E-A-D-B-C kromozomunun maliyeti ne?
C’den E’ye giden araç 30 birimlik mesafe katederken, E’den A’ya 30, A’dan D’ye 30, D’den B’ye 35, B’den C’ye geri dönerken ise 20 birimlik mesafe katedip toplamda 145 birimlik mesafe katetmiş oluyor. Bu durumda bu kromozomun maliyetini 145 birim olarak bulmuş oluyoruz.
Şimdi rastgele herhangi bir noktadan başlayarak tekrar aynı noktaya geri dönen toplam 5 adet kromozomumuzu oluşturalım.
- C-E-A-D-B-C=145
- E-B-A-D-C-E=120
- D-C-B-A-E-D=130
- A-B-C-D-E-A=130
- C-A-E-B-D-C=110
Bu çözümler içerisinden en başarılısı 5. çözümdür çünkü minimum maliyet ondadır, aracın gideceği optimal minimum mesafeyi bulmamız gerektiğinden bu problem minimizasyon problemidir.
Çaprazlama İşlemi
Başlangıç popülasyonu içerisinden belirlenen oran kadar kromozomu-çözümü kullanarak yeni çözüm oluşturma işlemine çaprazlama adını veriyoruz.
Birçok çaprazlama yöntemi mevcut, bunlar;
- Tek Noktalı Çaprazlama (One-point Crossover)
- İki Noktalı Çaprazlama (Two-point Crossover)
- Çift Noktalı Sıralı Çaprazlama (Linear Order Crossover (LOX))
- Çevrim Çaprazlama (Cycle Crossover)
- Pozisyon Temelli Çaprazlama (Position-based Crossover)
- Basamak Temelli Çaprazlama (Order-based Crossover)
- Kısmen Haritalanmış Çaprazlama (Partially Mapped Crossover (PMX))
Bu yöntemler hakkında daha detaylı bilgi edinmek isterseniz aşağıdaki 1 numaralı akademik makaleye göz atabilirsiniz. Biz bu yöntemlerden çift noktalı sıralı çaprazlama yöntemini kullanacağız.
Çift noktalı sıralı çaprazlama yöntemi, rastgele seçtiğimiz 2 adet kromozom içerisinden rastgele ikişer adet nokta seçip seçtiğimiz bu iki nokta arasında kalan bölgeyi kromozomlar arasında geçiş yaptırarak yeni kromozom üretme yöntemi olarak isimlendirilebilir.
Çaprazlama oranı %80 olduğuna göre 4 adet çözümü çaprazlama için kullanacağız. Burada hangi çözümleri seçeceğimiz rastgele olarak da belirleyebiliriz ancak bizlere kolaylık oluşturması bakımından uygulayabileceğimiz farklı yöntemler de mevcut. Bu yöntemler:
- Sıralama Yöntemi: Küçükten büyüğe doğru sıralanıp veyahut herhangi bir sıralama yapılmadan rastgele seçme yöntemi.
- Turnuva Yöntemi: Mesela rastgele 3 tanesini seçip bunlar arasından en iyi iki tanesini alma yöntemi
- Rulet Tekerleği Yöntemi: Çözümler başarı seviyelerine göre rulet tekerleğine yerleştirilir. Aralarından rastgele seçim yapılır.
Yukarıdaki yöntemler literatürde en çok kullanılan 3 yöntemdir. Bu ve buna benzer farklı seçim yöntemlerinin izahı ve karşılaştırılmasının yapıldığı 3 numaralı kaynaktaki (Uygun Arazinin Seçimi için Genetik Algoritmadaki Seçim Yöntemlerinin Belirlenmesi) konferans bildirisine ve 4 numaralı kaynaktaki (Genetik Algoritmalar için Seçim Metotları) adlı akademik yayına göz atıp bu yöntemler ile alakalı detaylı bilgi sahibi olabilirsiniz.
İki noktalı çaprazlama yöntemini rastgele seçtiğimiz 1. ve 4. çözümü kullanarak uygulayalım. Bu çözümler içerisinden yine rastgele seçeceğimiz 2. ve 4. düğümlerle düğümü 3 ayrı parçaya ayıralım.
C-E-2–A-D-4-B-C
A-B-2–C-D-4-E-A
Koyu renkle işaretlenmiş rastgele seçilen iki düğümün arasında kalan bölgeyi; üst kromozomun parçasını alta, alt kromozomun parçasını üste yazarak değiştireceğiz. Alttaki kromozomun CD parçasını yukarı çıkardığımızda sırasıyla soldan sağa kontrollerini genlerin parçada olup olmadığının kontrolünü gerçekleştiriyoruz. C geni CD parçası içerisinde mevcut ancak E geninin CD parçası içerisinde bulunmadığını görüyoruz bu yüzden en başa E genini yazacağız. Soldan sağa doğru ilerlediğimizde A geninin CD parçası içerisinde bulunmadığını görüyoruz bu yüzden E geninden sonra A genini yazacağız. D geni CD parçası içerisinde mevcut B geni ise parça içerisinde bulunmadığından dolayı CD’nin yanında B genini yazacağız. Son olarak oluşan yeni kromozomumuz E-A-C-D-B-E şeklinde oluşmuş oluyor. Aynı metodu alttaki kromozom için de uygularsak B-E-A-D-C-B şeklinde yeni kromozom oluşmuş oluyor.
Yeni kromozomlar ve
E-A-C-D-B-E =110
B-E-A-D-C-B =115
Rastgele 2 adet kromozom daha seçelim ve bunlar üzerinde de çaprazlama işlemini gerçekleştirip kromozom üretelim.
E-B-2–A-D–4-C-E=120
D-C-2–B-A–4-E-D=130
Çift noktalı sıralı çaprazlama yöntemini kullandıktan sonra oluşan yeni kromozomlar;
C-B-A-D-E-C=135
E-D-B-A–C-E=130
Popülasyonun %80’ine tekabül eden 4 adet kromozomun çaprazlama işlemini oluşturduk. Oluşan yeni kromozomlar algoritmanın doğal seleksiyon aşamasında bizlere yardımcı olacak ancak o aşamadan önce mutasyon işlemiyle farklı bir yöntem kullanarak yeni kromozomlar oluşturalım.
Mutasyon bir kromozomun gen sıralamasının değiştirilmesiyle farklı bir kromozom oluşturma işlemidir.
İlk kromozomu kullanarak yer değiştirme metoduyla 3. ve 4. genlerin yerlerini değiştirerek yeni bir kromozom elde edelim.
C-E-A–D-B-C=145 —-> 1. Kromozom
C-E-D–A-B-C=135 —-> Oluşan Kromozom
Yaptığımız tüm bu işlemlerden sonra elde ettiğimiz tüm kromozomları alt alta koyup başarısı en yüksek olan 5 tanesini alıp bitiriyoruz. Eğer istiyorsak bu 5 taneyi tekrar algoritmaya sokabiliriz.
- C-E-A-D-B-C=145
- E-B-A-D-C-E=120
- D-C-B-A-E-D=130
- A-B-C-D-E-A=130
- C-A-E-B-D-C=110
- E-A-C-D-B-E =110
- B-E-A-D-C-B =115
- C-B-A-D-E-C=135
- E-D-B-A-C-E=130
- C-E-D-A-B-C=135
10 tane kromozom arasında en kısa mesafeye gidenler maliyeti en düşük olanlar olduğuna göre bunlar sırasıyla 2., 5., 6.,7. ve 9. olarak alabiliriz. Son kromozomu hepsi 130’a eşit olduğu için rastgele 9. kromozom olarak aldım. Siz isteseniz maliyeti 130′ eşit başka bir kromozomu da 5. kromozom olarak ekleyebilirsiniz.
- E-B-A-D-C-E=120
- C-A-E-B-D-C=110
- E-A-C-D-B-E =110
- B-E-A-D-C-B =115
- E-D-B-A-C-E=130
Burada yaptığımız işlemleri grafik üzerinde gösterip yaptığımız çaprazlama ve mutasyon işleminin amacını daha net bir şekilde görebiliriz. Çözmüş olduğumuz problemdeki çözümleri oluşturan kromozomların her birinin grafik üzerinde bir noktaya karşılık geldiğini varsayalım.
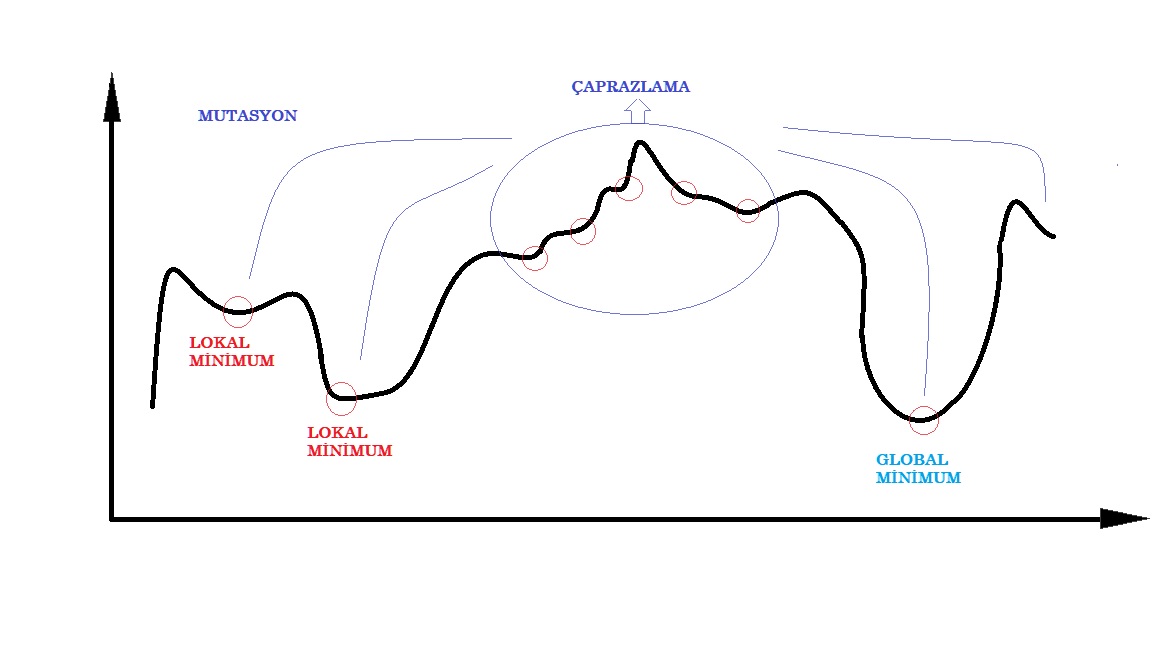
Her bir çukur noktasına lokal minimum noktası ismi veriliyor. Grafikteki en düşük ve bizim esas ulaşmak istediğimiz nokta ise global minimum noktası olarak adlandırılıyor. Çaprazlama işlemiyle iki çözüm noktası arasındaki veya çevresine göre daha başarılı olan komşu çözüm noktalarını buluyoruz. Eğer sadece çaprazlama işlemi yapsaydık komşu çözümler ve tek bir lokal minimum değer arasında kalırdık. Mutasyon işlemi ise bizlere bu lokal minimum değerler arasında sıçrama yapmamızı sağlıyor ve lokal minimum değerlerine takılıp o değerler arasında kalmamızı engelliyor. Mutasyon operatörüyle algoritmanın (grafiğin) farklı yerlerine sıçramalar gerçekleştirebiliyorum. Genetik algoritmada yerel arama (çaprazlama) için belirlenen parametre değerleri %80-%95 arasında, genel arama (mutasyon) için belirlenen parametre değeri %5-%20 arasındadır. Genetik algoritmada global ve lokal minimum noktaları ile alakalı 2 numaralı kaynaktaki uygulamalı Matlab örneğine göz atabilirsiniz.
Peki bu algoritmadaki REPEAT-UNTİL döngüsü ne zamana kadar devam edip ne zaman sonlanacak?
Burada 3 tane yöntem kullanıyoruz.
- Belirlenen iterasyon (çevrim sayısı) kadar: Mesela 1000 iterasyondan yapsın sonra dursun istiyoruz
- İyileşme periyodu kadar: Eğer belirlenen iterasyon sayısı kadar çevrim yapıp daha iyi bir çözüm üretemiyorsa algoritmanın aramasını durdurmasını sağlayabiliriz.
- Kabul edilebilir hata seviyesi kadar: Belli bir hata seviyesinin altına inmiş çözümler kabul edilebilir sayılırsa.
Kaynakça:
- https://www.researchgate.net/publication/304400311_A_Study_of_Crossover_Operators_for_Genetic_Algorithm_and_Proposal_of_a_New_Crossover_Operator_to_Solve_Open_Shop_Scheduling_Problem
- Global vs. Local Optimization Using ga – MATLAB & Simulink (mathworks.com)
- Determination of Selection Method in Genetic Algorithm for Land Suitability (matec-conferences.org)
- (PDF) Selection Methods for Genetic Algorithms (researchgate.net)

